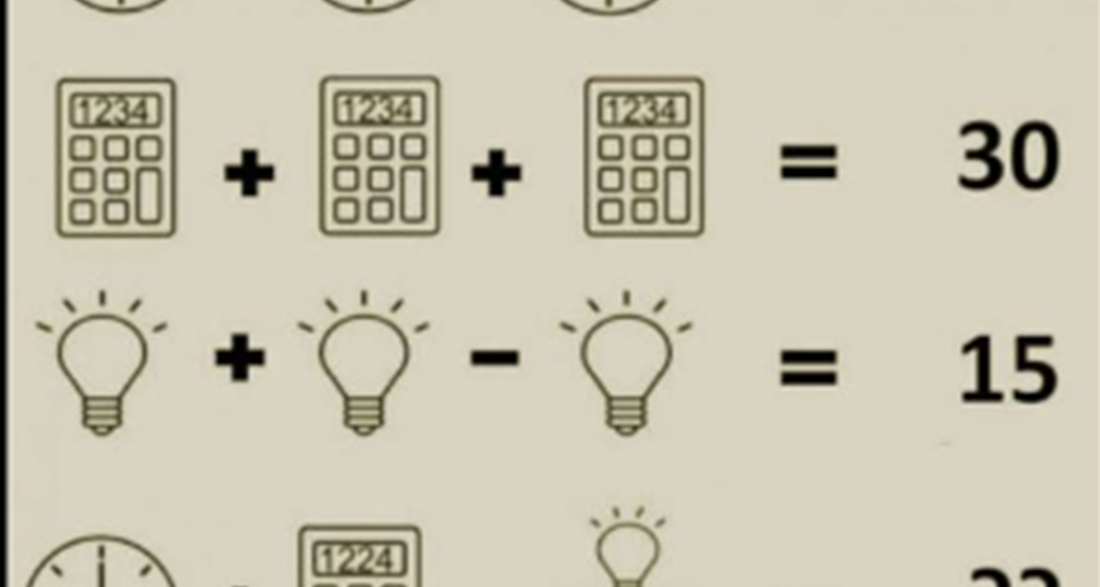
Let’s dive into solving this intriguing puzzle with clocks, calculators, and bulbs.
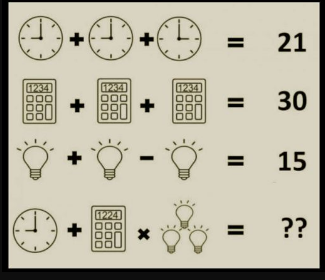
Firstly, we establish the value of one clock using the information from the first equation. Adding up three clock times: 9 o’clock + 9 o’clock + 3 o’clock gives us 9 + 9 + 3 = 21. Therefore, the value of one clock is 7 (since 21 divided by 3 clocks equals 7).
Moving on to the second equation involving calculators. It states that three calculators together equal 30. So, one calculator must be 30 divided by 3, which equals 10. Additionally, the sum of the numbers inside a calculator (1 + 2 + 2 + 4) equals 9.
Now, let’s tackle the third equation involving bulbs. It states that one bulb plus another bulb minus one bulb equals 15. Simplifying, we get 1 bulb with five lights equals 15. Thus, one bulb with one light is 3 (since 15 divided by 5 equals 3). Therefore, a bulb with four lights equals 4 times 3, which equals 12.
Now, putting it all together into the final equation: 9 o’clock + Calculator (1 + 2 + 2 + 4) times 3 bulbs (each with four light rays). Translating this into numbers: 9 + (1 + 2 + 2 + 4) x 3 x 12. Calculating further: 9 + 9 x 36 = 9 + 324 = 333.
Therefore, the final value derived from all these equations and calculations is 333.
This puzzle challenges us to think logically and use math skills to find the values of clocks, calculators, and bulbs. Each step leads us closer to the intriguing final answer of 333.
Did you manage to solve this puzzle? Let us know in the comments down below!